완전 이진 트리(complete binary tree)의 특징
0. 완전 이진 트리에서는 다음과 같은 관계가 성립:
n0 = n2 + 1
여기서,
- n0 : 리프 노드(leaf node)의 개수
- n2 : 2개의 자식 노드를 가진 내부 노드(internal node)의 개수
간단한 증명 :
n= n0 + n2
n-1 = 2(n2)
이 두 식을 정리하면 n0 = n2 + 1
1. 모든 레벨의 노드가 꽉 차 있다.
- 마지막 레벨을 제외하면, 모든 레벨의 노드가 채워져 있다.
( 각 내부 노드는 무조건 자식 노드를 2개 가져야 한다. )
2. 완전 이진 트리의 마지막 레벨은 이전 레벨들과 달리 불완전할 수 있으나, 이 때 마지막 레벨의 노드들은 왼쪽에서 오른쪽 방향으로 순서대로 채워져야 한다.
( 마지막 레벨 노드 개수는 2^(h-1)이하일 것 )
- 왼쪽 자식 하나만 있어도 왼쪽에서 오른쪽으로 채워져야 한다.
- 아래의 그림과 같은 형태가 완전 이진 트리의 예시들이다.

3. 노드의 개수가 n개일 때, 노드 인덱스 범위는 다음과 같다.
- 리프 노드 인덱스 범위 : n/2 ~ n-1
- 내부 노드 인덱스 범위 : 0 ~ n/2- 1
4. 완전 이진 트리는 배열로 표현하기 쉬워 레벨 순회가 효율적이다.
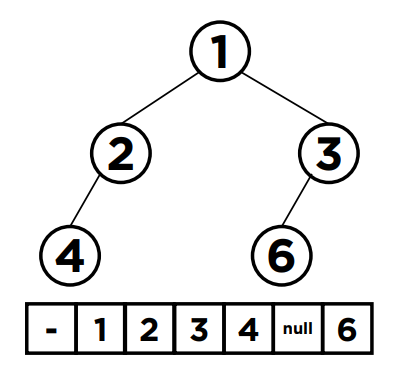
위 그림은 중간에 빈 값이 있는 이진 트리를 배열로 표현한 것이다.
5. 완전 이진 트리에서는 각 노드의 왼쪽 자식 노드와 오른쪽 자식 노드의 인덱스가 다음과 같다.
- 왼쪽 자식 노드 인덱스 : 2*i + 1
- 오른쪽 자식 노드 인덱스 : 2*i + 2
( 여기서 i는 현재 노드 인덱스)
위 내용이 성립하는 이유는 완전 이진 트리는 각 레벨의 노드들이 왼쪽부터 빈틈없이 채워지기 때문.
'자료구조' 카테고리의 다른 글
| [자료구조] 문자열 radix sort algorithm 문제풀이 (2) | 2024.06.09 |
|---|---|
| [자료구조] 기수 정렬(radix sort) 문제 풀이 (18) | 2024.06.05 |
| [자료구조] 힙 정렬(Heap Sort) 문제 풀이 (2) | 2024.06.04 |
| [자료구조] 인접 행렬과 인접 리스트 문제 풀이 2 (23) | 2024.05.26 |
| [자료구조] 인접 행렬과 인접 리스트(adjacency list) 문제 풀이 1 (1) | 2024.05.26 |