기수 정렬 (radix sort)
: 실제 숫자들 간의 비교를 통해 정렬을 하는 것이 아니라, 버킷(bucket) 을 이용해 정렬하는 방법.
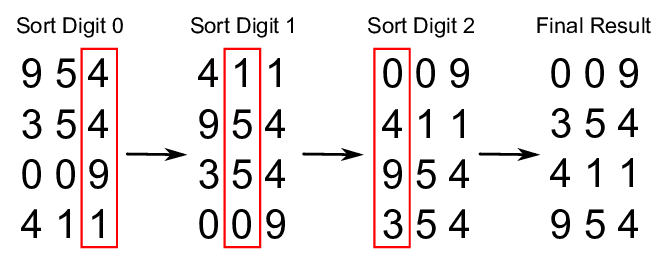
각 자릿수 별로 0~9까지의 버킷이 있고, 이 버킷에 순서에 맞게 숫자를 넣어가며 분류한다고 생각하면 된다. 우리는 LSD를 사용할 것이므로, 일의 자리 수부터 시작한다.
위 그림을 더 이해하기 쉽게 적어보자면,
1. sort digit 1 : [411], [954,354] , [009]
2. sort digit 2 : [009], [411], [954,354]
3. sort digit 3 : [009], [354], [411]. [954]
가 되겠다. 가장 낮은 1번째 자리부터 가장 높은 3번째 자리 순으로 정렬하였다. (LSD)
이제 Radix sort algorithm(LSD)를 이용하여 코드를 작성해야 하는 문제를 함께 살펴보자. 아래 문제는 두 자리 숫자를 radix sort algorithm을 통해 정렬해야 하는 문제이다.

필자는 라딕스 정렬 과정에 있어서 f, r, a 3개의 배열을 사용하였다.
int f[10] = {0}; // 각 자릿수의 빈도 수를 저장하는 배열
int r[n]; // 정렬된 결과를 임시로 저장하는 배열
int a[n]; // 입력 배열
f 배열은 각 digit의 빈도를 저장하는 배열이다. 예를 들어 1의 자리에서 f[3]=5라면, 1의 자리에 3이 위치한 요소가 5개 있다고 해석할 수 있겠다.
// 각 자릿수의 빈도 수 계산
for (int i = 0; i < n; i++) {
int digit = (a[i] / ((int)pow(10, d-1))) % 10;
f[digit]++;
}
n은 전체 요소 개수, d는 현재 digit index를 의미한다. d=1일 때로 생각해 보면, 위 for문을 통해 1의 자리의 0~9 각각의 빈도 수를 구할 수 있게 되며, 이는 모두 배열 f에 저장된 상태가 될 것이다.
위 과정을 통해 배열 f를 구한 후,
// 누적 합 계산
for (int i = 1; i < 10; i++) {
f[i] += f[i-1];
}
위 코드와 같이 누적 합을 계산하는 과정이 필요하다. 위 코드를 통해, 이를테면 f[3]은 숫자 0~3까지의 누적 빈도 값을 가지게 될 것이다. 여기서 눈치 챘을 지 모르겠지만, 이 f 배열 자체를 새로운 정렬의 index로 사용할 예정이다. 바로 아래와 같이 말이다.
* 이해하는 데 다소 시간이 걸릴 수 있는 코드 *
// 정렬된 결과를 r 배열에 저장
for (int i = n-1; i >= 0; i--) {
int digit = (a[i] / ((int)pow(10, d-1))) % 10;
r[--f[digit]] = a[i];
}
d=1일 때, 위 코드를 통해 r 배열에는 a 배열의 일의 자리 수가 정렬된 형태로 저장되게 된다. i=n-1부터 시작해서 줄여나가는 이유는, 우리는 앞서 구해둔 누적값을 index로 사용할 것이기 때문이다. 앞서 살펴본 예시로 치자면, [411], [954,354] , [009]의 순서로 말이다. 그런데 우리 문제에서는 십의 자리 수까지만 다루기 때문에, 지금까지 우리가 해 온 과정을 한 번 더 반복(d=2) 해주면 정렬이 완료된다. 일의 자리 수의 정렬을 완료한 r배열을 가지고 다시 한번 십의 자리 수의 정렬을 진행해 주는 것이다.
아래에 전체 정답 코드를 남겨두며 포스팅을 마친다.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define MAX_DIGIT 2 // 각 정수는 0~9의 숫자 2개로 구성됨
// 라딕스 정렬 함수
void radix_sort(int arr[], int n) {
int f[10] = {0}; // 각 자릿수의 빈도 수를 저장하는 배열
int r[n]; // 정렬된 결과를 임시로 저장하는 배열
int a[n]; // 입력 배열
// 입력 배열 복사
for (int i = 0; i < n; i++) {
a[i] = arr[i];
}
// 최대 자릿수까지 반복
for (int d = 1; d <= MAX_DIGIT; d++) {
// 각 자릿수의 빈도 수 계산
for (int i = 0; i < n; i++) {
int digit = (a[i] / ((int)pow(10, d-1))) % 10;
f[digit]++;
}
// 누적 합 계산
for (int i = 1; i < 10; i++) {
f[i] += f[i-1];
}
// 정렬된 결과를 r 배열에 저장
for (int i = n-1; i >= 0; i--) {
int digit = (a[i] / ((int)pow(10, d-1))) % 10;
r[--f[digit]] = a[i];
}
// 다음 자릿수 정렬을 위해 a 배열 업데이트
for (int i = 0; i < n; i++) {
a[i] = r[i];
}
// f 배열 초기화
for (int i = 0; i < 10; i++) {
f[i] = 0;
}
}
// 정렬된 결과 출력
for (int i = 0; i < n; i++) {
printf("%d ", a[i]);
}
printf("\n");
}
int main() {
int arr[11];
int n = 0;
// in.txt 파일에서 정수 읽기
FILE *fp = fopen("in.txt", "r");
if (fp == NULL) {
printf("파일 열기 실패\n");
return 1;
}
while (fscanf(fp, "%d", &arr[n]) != EOF) {
n++;
}
fclose(fp);
// 라딕스 정렬 수행
radix_sort(arr, n);
return 0;
}'자료구조' 카테고리의 다른 글
| [자료구조] BST insert, inorder traversal 문제 REVIEW (3) | 2024.06.10 |
|---|---|
| [자료구조] 문자열 radix sort algorithm 문제풀이 (2) | 2024.06.09 |
| [자료구조] 힙 정렬(Heap Sort) 문제 풀이 (2) | 2024.06.04 |
| [자료구조] 완전 이진 트리(complete binary tree)란? (1) | 2024.06.04 |
| [자료구조] 인접 행렬과 인접 리스트 문제 풀이 2 (23) | 2024.05.26 |